Hello World
Many online introductions to neural networks tend to be technical or rely on frameworks. However, there’s a simpler way to dive into the world of neural networks by implementing a basic “Hello World” program. In this article, we’ll take you through a step-by-step process of building a straightforward neural network with just one neuron.
What is Artificial intelligence?
There are lots of definition of AI in web, but the simplest term how I think of AI is, it’s a different paradigm of programming where we program a machine to attain a certain goal from a certain data.
So as in other paradigm of programming where we tell the computer step-by-step to achieve a certain goal, but in AI we don’t tell the computer programming how to do a certain task, but we write the program that train the AI to do certain task.
It would become more clearer as we proceed through the basic “Hello World!” program.
Language we will use
To create the simplest neural network we will use JavaScript. I know JavaScript is not a performant language but for our simplest task it’s fine, also most of programmer are familiar of JavaScript.
The problem
Our program is very simple let say you have been given a series of tuple where first element is the input and the second element is the desired output, now you have to write a program that can predict the output if you give any input other than the input provided.
1
2
3
const input = [
[0, 0], [1, 2], [2, 4], [3, 6], [4, 8]
];
Since the input is very small so we can tell the answer will be y = x * 2, but it will be not easy to guess if you have millions of data. But from the data we can say the equation will be something like \(y = x \times weight\).
The Neuron
In our case we need a very simple neuron which will take one input and spits our one output, and to train the model we will use a Weight and a Bias. 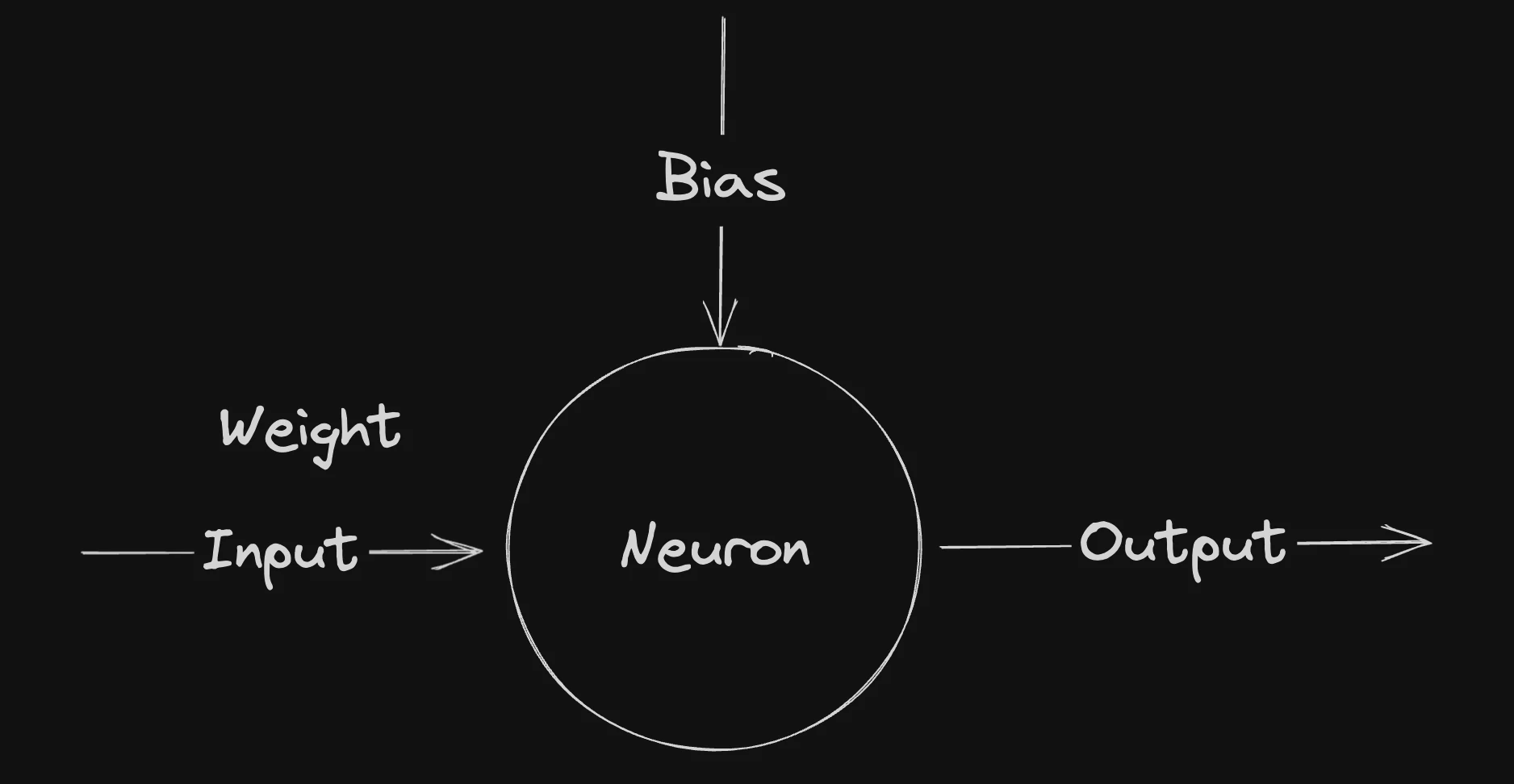
Actual programming
So our Equation is y = x * w where w is the weight we need to find out.
1
2
3
4
// let take a random weight between 0 to 10
let weight = Math.random() * 10; // let say you got 5
// now let's pass the weight into the Equation, input is defined in above code snippet
const y = input[1][0] * weight; // y will be 5
Cost function
In the above code we are calculating the result of one input, but we have to do it for all input values to get the real difference. We will create a cost function for this will will give the average distance from the real value.
1
2
3
4
5
6
7
8
9
10
11
function cost(weight) {
result = 0;
for (let i = 0; i < input.length; i++) {
const x = input[i][0]; // actual input
const y = input[i][1]; // actual output
const calculatedResult = x * weight; // the result we have calculated from the weight
const distance = calculatedResult - y; // the difference between the actual value and the calculated value
result += distance * distance; // squaring the diff to remove negative and increase the difference so it is visible clearly
}
return result / input.length;
}
This cost function gives us idea how much we are away from the actual value so in order to get the correct result we need to reduce the cost function. Now to minimise the cost function we can use derivative as it will give the direction for us to get the local minimum.
Derivative
The real derivative
\(f'(x) = \lim\limits\_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}\)
It’s very hard to implement so for now we will go with Finite difference which is The approximation of derivatives, central difference is the most used one.
Finite difference
Finite difference Wiki
equation for central difference is as follows
\(f'(x) = \frac{f(x + h) - f(x - h)}{2h}\)
reducing the cost function
Now we can get the partial derivative of the cost function with respect to weight is as follows
1
2
3
const h = 0.001;
const dw = ((cost(wieght + h) - cost(weight - h)) / 2) * h;
weight -= dw; // this will adjust the weight to get to the local minimum.
Training
The training is very simple just loop through the reducing the cost function for certain no of time.
1
2
3
4
5
6
const iter = 1000; // we will adjust the weight 1000 time
learningRage = 0.001; // we need to have a learning rate to reduce the changes in the weight
for (let i = 0; i < iter; i++) {
const dw = (cost(wieght + h) - cost(weight - h)) / (2 * h);
weight -= learningRage * dw; // this will adjust the weight to get to the local minimum.
}
Final Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const input = [
[0, 0], [1, 2], [2, 4], [3, 6], [4, 8]
];
// let take a random weight between 0 to 10
let weight = Math.random() * 10;
function cost(weight) {
result = 0;
for (let i = 0; i < input.length; i++) {
const x = input[i][0]; // actual input
const y = input[i][1]; // actual output
const calculatedResult = x * weight; // the result we have calculated from the weight
const distance = calculatedResult - y; // the difference between the actual value and the calculated value
result += distance * distance; // squaring the diff to remove negative and increase the difference so it is visible clearly
}
return result / input.length;
}
const h = 0.001;
const learningRage = 0.001;
const iter = 1000; // we will adjust the weight 1000 time
for (let i = 0; i < iter; i++) {
const dw = (cost(weight + h) - cost(weight - h)) / (2 * h);
weight -= learningRage * dw; // this will adjust the weight to get to the local minimum.
console.log(`Weight: ${weight}, cost: ${cost(weight)}`);
}
console.log(`Final weight: ${weight}`);
For this input the Final weight would be closed to 2, also if you change the input the output will change accordingly.
